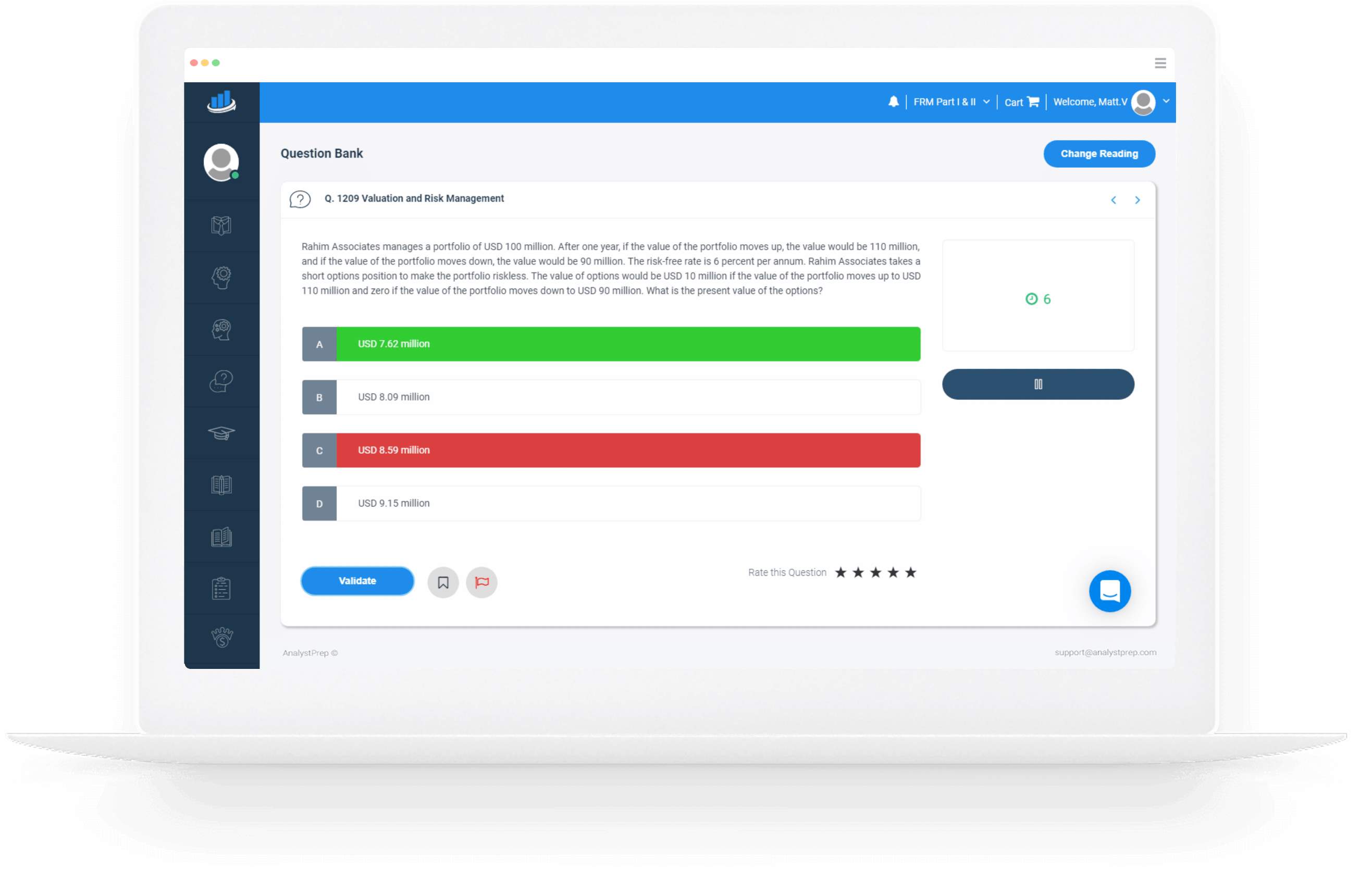
题库、模拟考试、学习笔记和视频课程
用于CFA®,FRM®和SOA®考试的研究材料
由Analystrep提供

欢迎来到分析秘密
CFA的#1级准备平台®程序与FRM®程序
带上你的学习经验新的高度与分析专家

3.5
百万
我们的用户回答的问题
50
千
满意的客户
#
1.
评分为
评审网站CFA准备平台
分析人员代表终审法院®程序